Measurement Computing Corporation (MCC) and Data Translation (DT) DAQ products are now part of the Digilent family of test and measurement solutions. MCC and DT are leading suppliers of data acquisition solutions that are easy-to-use, easy-to-integrate, and easy-to-support.
Data Acquisition & Data Loggers
DAQ and Data Logger solutions from Measurement Computing and Data Translation provide for a wide range of applications and interfaces. Whether you are measuring current, voltage, temperature, strain or digital signals, these products offer high-quality hardware with accompanying software and drivers for a quick and customizable solution for your unique application.
OEM Board-Only
As a leading supplier of OEM DAQ solutions, we offer high-quality, cost-effective products backed by a worldwide sales and support network.

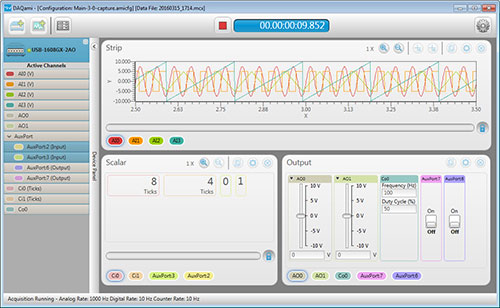
DAQ Software
Software for Measurement Computing devices includes easy-to-use data viewing and logging software, drivers for the most popular applications and languages, and support for Windows® and Linux®. MCC out-of-the-box software provides the ability to log and view data and generate signals. Drivers are included for the most popular applications and programming languages.
Accessories
MCC has a wide range of accessories, including mounting hardware, thermocouples, power supplies, and more to enhance productivity.
Legacy DAQ Products
Though legacy DAQ devices are not recommended for new applications, they are robust and reliable.

MCC Files
Files from the original MCC FTP site can be found on the Digilent files site.












